This article explores writing a third-order inviscid Euler solver as the final project for Georgia Tech’s AE6042 Computational Fluid Dynamics. All the material used to create this is within the GitHub repository.
Summary
A more detailed review of the project set-up and results are covered in the report. The following is just a brief summary showing some of the images and highlighting some of the skills developed/utilized in the project. This is not intended to be a comprehensive review of the theory or implementation of a CFD solver.
The final project for Georgia Tech’s graduate CFD course was to write a CFD solver. When I took the class in spring of 2023, the specific task was to resolve the shock that develops on the top half of a 2D, supersonic, diamond-shaped airfoil. The mesh was provided by Professor Oefelein, and is shown in Figure 1.
Figure 1: Mesh
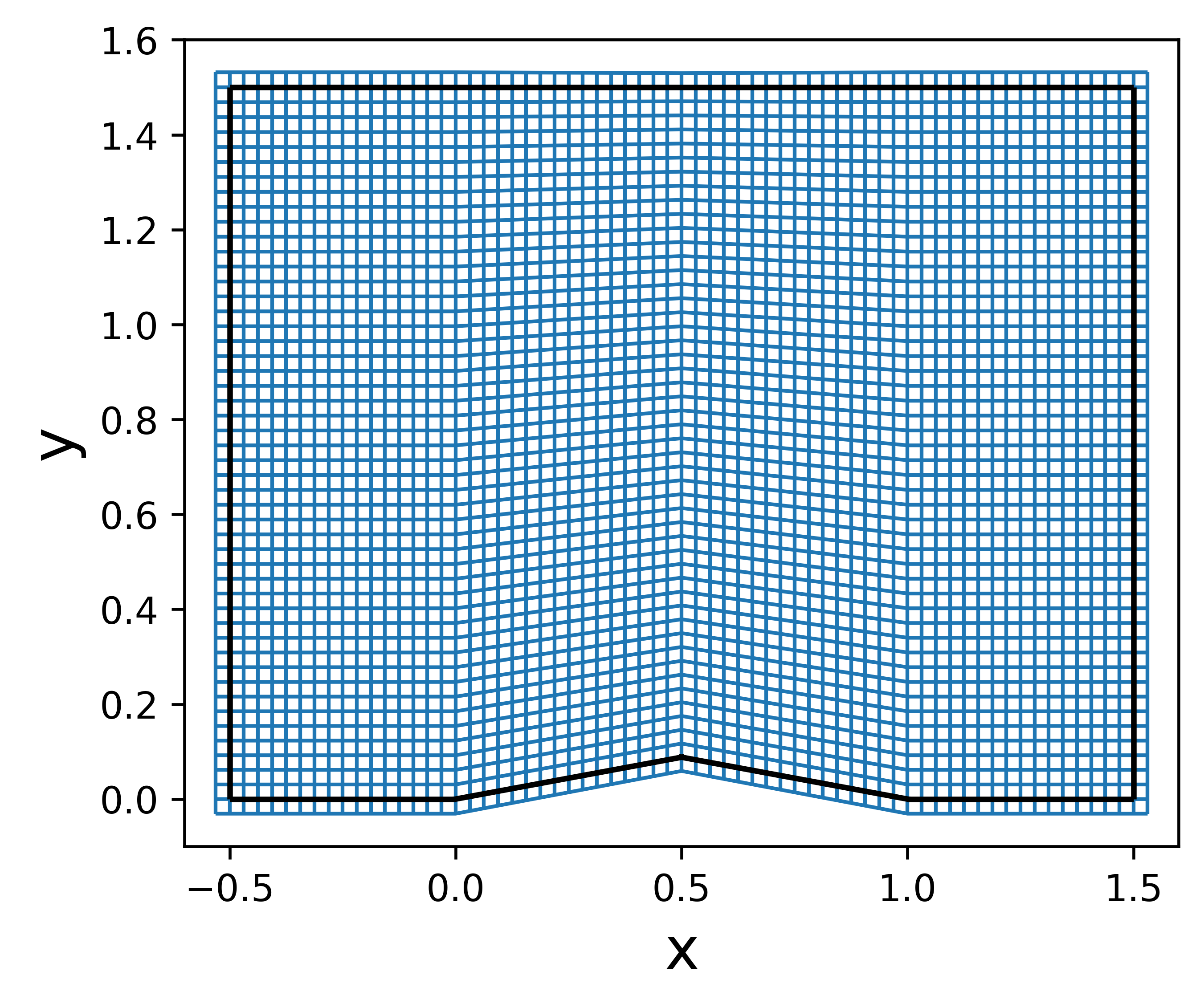
The actual relevant domain is outlined in black. The cells on the outside of the domain are the so-called ‘halo cells’ which are used to enforce boundary conditions. Note how the mesh forms a pyramid shape in the center. That is the the top half of the diamond airfoil.
The boundary conditions applied to the mesh were equivalent to an aircraft traveling at Mach 2 from right to left at sea level. Thus, the static pressure and temperature were 1 atmosphere and 300K respectively. To make a long story short, I wrote the solver utilizing a computationally fast software architecture described below and plotted the results. Again, if you want more details, see the report.
Figure 2: 3rd Order Accurate QUICK Scheme Solution
Note: This image is very high resolution and if you right click it and open it in a new tab you can zoom in without losing fidelity.
The key feature to note in the plots is the defined shock wave visible in all of the subplots in Figure 2. This showed that the solver was capable of resolving the discontinuity in flow properties located at the shock wave without diverging. The flow properties calculated could be used to guide airfoil design for supersonic aircraft, and more complex solvers are a cornerstone of modern aerodynamic design.
Interesting Concepts
Euler Equations
The Euler equations stand as a cornerstone in the realm of fluid dynamics, capturing the fundamental principles governing the motion of inviscid fluids. Named after the 18th-century Swiss mathematician Leonhard Euler, these partial differential equations elegantly describe the conservation of mass, momentum, and energy in fluid systems. The Euler equations have found applications in various fields, from aerospace engineering to meteorology, providing a mathematical framework to analyze and predict fluid behavior. Understanding these equations is pivotal for grasping the intricacies of fluid flow, making them an indispensable tool for engineers and scientists alike.
Finite Volume Method
In the quest to numerically solve partial differential equations, the Finite Volume Method (FVM) emerges as a powerful approach, particularly well-suited for modeling fluid dynamics. FVM discretizes the governing equations by dividing the computational domain into discrete control volumes, allowing for a localized and conservative representation of physical quantities. This method has proven to be versatile, handling complex geometries and unstructured grids with ease. As simulation technologies advance, FVM stands out for its ability to strike a balance between accuracy and computational efficiency, making it an indispensable tool for engineers tackling real-world fluid flow problems.
Just-in-Time Compilation
Just-in-Time (JIT) compilation has revolutionized the way we approach performance optimization in computing. It involves compiling code at runtime rather than ahead of time, allowing for dynamic adaptation to the underlying hardware. In the realm of scientific computing and numerical simulations, Numba shines as a JIT compiler for Python. Developed by Anaconda, Numba translates Python functions into machine code on-the-fly, significantly accelerating the execution of numerical algorithms. This approach enables researchers and engineers to seamlessly integrate high-level Python code with the performance of low-level languages, opening new avenues for the rapid development of efficient and scalable scientific applications.
Rust
Rust, a programming language born out of a Mozilla Research project, has rapidly gained popularity for its unique blend of performance, memory safety, and modern syntax. Designed to be a systems programming language that prioritizes both developer productivity and low-level control, Rust offers a compelling alternative for those seeking a reliable and efficient toolset.
At the core of Rust’s appeal is its ownership system, a groundbreaking approach to memory management. The ownership system ensures memory safety without the need for a garbage collector, preventing common bugs like null pointer dereferences and data races. This makes Rust particularly attractive for systems-level programming where low-level control over resources is crucial, all while mitigating the risk of memory-related errors.
Beyond its safety features, Rust excels in performance. Its zero-cost abstractions allow developers to write code that is both elegant and efficient. With a focus on providing predictable performance, Rust is well-suited for a range of applications, from embedded systems to web development and beyond.
Python Libraries
Numpy
Numpy is a powerhouse in scientific Python analysis, and needs no introduction.
Numba
Numba is a ‘just-in-time’ compiler for Python which compiles code to make it run at speeds comparable to C or FORTRAN. Numba was necessary to increase the run time of the solver by >100x.
Tqdm
Tqdm is just a progress bar library. I like to use it to let me know how long my scripts are taking.
Note: An environment.yml file is included in the GitHub repository to allow you to recreate a functional Anaconda environment.
Highlighted Code Architecture
Python
The Python code was structured such that JIT compilation with Numba was could be implemented. This was planned before beginning the project, as I knew Python is slow in its implementation of for-loops, and it would be difficult to optimize the code solely with Numpy vectorization. The code had the following outline:
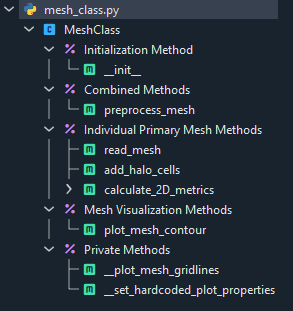
Mesh Class
The mesh class was written to load the structured mesh from a text file, add halo cells, and calculate various statistics such as cell areas and wall vectors. It also contained a mesh visulization method which created the plot shown in Figure 1. Figure 3 below shows the Spyder outline of the mesh.
Figure 3: Mesh Outline
Solver Class
The solver class contained the main logic to implement the finite-volume method to solve the inviscid Euler equations. Figure 4 contains the Spyder outline of the code.
Figure 4: Solver Outline
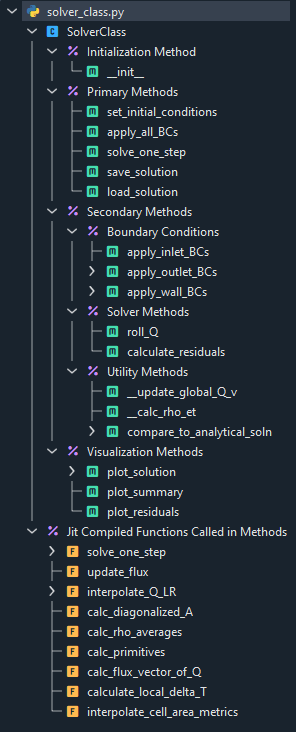
As shown in the outline, the solver class contained primary, secondary, and visualization methods. The primary and visualization methods are intended to be called by the user, whereas the secondary methods are internal to the solver. This was written before I really knew about private methods and attributes, and that could be used to improve the code.
The visualization methods were used to create the plots such as Figure 2 which show the solution and convergence history at the current timestep.
External to the solver were the JIT compiled functions. These functions implemented the actual solution logic as for-loops so that they were easy to understand, but the functions were decorated with the @njit decorator to compile the code to run orders of magnitude faster.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
@njit
def update_flux(
Q: ndarray[(2, ..., ...,4), np.float64],
flux: ndarray[(...,...), np.float64],
flux_direction: str,
S_x, S_y, S, delta_V, # Area and volume components, can be either xsi or eta
gamma: float,
epsilon: int,
kappa: float,
flux_limiter_type: str,
) -> ndarray[(...,...), np.float64]:
"""A function to calculate the flux over a single face. The flux matrix will be padded with zeros since those
correspond to halo cell fluxes that we don't care about. I'm leaving them there for ease of indexing.
This updates the input vector flux in-place, but also returns it for good measure. """
# See the processed indexed mesh diagram. The (0,0) row and column are all exterior cell boundaries, so we
# can skip the 0th index. The
for i in range(1, S.shape[0]-1): # Every row, skip the halo cells
for j in range(1, S.shape[1] - 1): # Every column, skip the halo cells
# Determine Q_left and Q_right for that wall, in either the xsi or the eta 'flux direction'
Q_LR = interpolate_Q_LR(
Q,
i,
j,
mode = flux_direction,
epsilon = epsilon,
kappa = kappa,
limiter_type = flux_limiter_type
)
# Calculate Roe Averages of Properties (xsi direction)
RA_xsi = calc_rho_averages(Q_LR, gamma)
# Calculate Diagonalized A at the Wall
L, lambda_ij, R = calc_diagonalized_A(
rho = RA_xsi[0], # Primitive components (rho_bar, u_bar, v_bar, h_t_bar, c_bar)
u = RA_xsi[1],
v = RA_xsi[2],
h_t = RA_xsi[3],
c = RA_xsi[4],
S_x = S_x[i, j],
S_y = S_y[i, j],
S = S[i, j], # Area components for the given direction
gamma = gamma,
)
# Take the absolute value of the eigenvectors and recombine A
A_bar = R @ np.abs(lambda_ij) @ L # / delta_V_bar
# Calculate E or F (fv for flux vector) based on the Left and Right Q vectors
fv_Q_LR = calc_flux_vector_of_Q(
Q_LR = Q_LR,
S_x = S_x[i,j],
S_y = S_y[i,j],
S = S[i,j], # Area components
gamma = gamma,
)
# Per Eqn 8 of the Topic 25 Notes
flux[i,j] = (fv_Q_LR[:, 0] + fv_Q_LR[:, 1]) / 2 - A_bar @ (Q_LR[:, 1] - Q_LR[:, 0]) / 2
return flux
Rust
Shortly after writing the Python version of this solver, I wanted to learn Rust. I rewrote the solver logic in Rust, gaining a 100x speed improvement on top of the already optimized Python implementation. The Rust code is contained within the GitHub Repository.
Conclusion
This project expanded my understanding of computational fluid dynamics, and tested my software development skills, forcing me to learn new techniques to mitigate the runtime of the solver. Future work on this project could include adding the viscous terms to the solver to make it a full Navier-Stokes solvers.
Resources
The Report
Here is the final report written for the class which dives deeper into the set-up and results of the project.