Variational mode decomposition (VMD) was explored as a methodology for denoising data, based on prior work by (Chen et al.). An artificial dataset was generated with both clean and noisy signals, and then VMD performed on the signals while varying the VMD hyperparemeters α and k. The signal to noise ratio (SNR) as described by the paper was used to characterize the proficiency in denoising. Two SNRs were obtained for each set of VMD hyperparameters: estimated SNR, which compares the denoised signal to the noisy signal, and true SNR, which compares the denoised signal to the original clean signal. It was discovered that the paper’s methodology for denoising was overly conservative in removing noise and its optimization would settle upon the VMD hyperparameters that least changed the signal fed to the algorithm leaving room for a 25% improvement in true signal to noise. Ultimately, VMD was essentially just functioning as a low-pass filter and alternative methods such as a rolling average or a Butterworth filter would be simpler, more widely used, and easier to understand.
Introduction
Context
Something I noticed in the Combustion organization at GE is that we had terabytes of time series data, but we only actually used steady state sections of that data that were manually identified on the day of the test. Seeing this, I endeavored to create a Python tool which would comb through the existing data GE had and locate additional steady state points that we could use to increase our confidence in characterizing our combustor performance. We already paid for the data; why not get our money’s worth?
After researching methods for steady state detection, I stumbled across variational mode decomposition (VMD) as a method for preprocessing real-world, noisy data, before proceeding with the steady state detection.
In sum, the paper (Chen et al.) describes a technique for using Bayesian optimization to choose the optimal hyperparameters for VMD such that the denoised signal captures a large amount of the variation of the original noisy signal, while having less Gaussian noise. I explored the optimization to understand the effects of the hyperparameters and the ultimate results.
Interesting Concepts
Variational Mode Decomposition
Variational Mode Decomposition (VMD) is a powerful signal processing technique that aims to decompose a complex signal into a sum of simpler oscillatory modes. Unlike traditional methods such as Fourier analysis, VMD does not rely on predefined basis functions. Instead, it formulates the decomposition as an optimization problem, seeking modes that are both sparse and well-localized in the time-frequency domain. This approach makes VMD particularly effective for extracting hidden patterns and structures in signals with non-stationary and nonlinear characteristics. VMD has two primary hyperparameters, α and k.
Alpha (α): Definition: Alpha is a key hyperparameter in VMD that sets the mode bandwidth limit criterion. It influences the width of the extracted oscillatory modes.
Effect: A higher alpha constrains the bandwidths of the modes, resulting in narrower modes that capture more localized frequency information. On the other hand, a lower alpha allows for broader modes that may capture broader frequency components.
K (Number of Modes):
Definition: K represents the number of modes that the VMD algorithm aims to extract from the input signal. It is a crucial hyperparameter as it determines the complexity of the decomposition and the number of oscillatory components in the final result.
Signal to Noise Ratio
The Signal-to-Noise Ratio (SNR) is a fundamental concept in signal processing and communication engineering. It quantifies the ratio of the power of a signal to the power of background noise. In other words, SNR provides a measure of how much the desired signal stands out from the surrounding noise. A higher SNR indicates a clearer and more reliable signal, making it easier to distinguish and interpret. SNR is a crucial metric in various applications, including telecommunications, audio processing, and image analysis, where the fidelity of the signal is of paramount importance.
Bayesian Optimization
Bayesian Optimization is an optimization technique commonly used for optimizing complex and computationally expensive functions. Unlike traditional optimization methods, Bayesian Optimization leverages probabilistic models to estimate the objective function and its uncertainty. By iteratively selecting the most promising points to evaluate, based on the current model, it efficiently navigates the search space to find the optimum with minimal function evaluations. Bayesian Optimization is particularly valuable in scenarios where each function evaluation is costly, such as in hyperparameter tuning for machine learning algorithms or optimizing parameters in scientific experiments.
Methodology & Results
I created two traces of representative data: pressure and temperature, using a script which allows me to draw the trace in MS Paint, then load it into Python, give it a time x-axis, and optionally add noise and outliers. For instance, below is the raw pressure trace as a PNG image. You might have to zoom in to see it; the trace is one pixel thick.
Figure 1: PNG Pressure Trace

Here are the plots of the generated signals. Notice how the pressure trace in Figure 2 matches the line in Figure 1 above.
Figure 2: Experimental Data Plot
Note: Try moving the plot around, zooming in, and clicking on legend entries. If you like these plots, look into Plotly which allows you to save interactive plots as .html files. You can also click on the Standalone Figure link to get a larger version of the figure.
From this point, α and k, the two primary hyperparameters of VMD, were varied. α is the bandwidth penalty, and k is the number of modes. Increasing α makes it so that each mode covers a smaller frequency band, and increasing k decomposes the original signal into more modes (see here for more details).
The original paper used VMD to decompose the signal into k modes, and then added together a subset of those modes that captured the majority of the variance of the original signal to create a reconstructed signal. An example of this signal reconstruction is shown in Figure 3 below.
Figure 3: Example of Decomposed and Reconstructed Signal
Notice how the first mode captures the majority of the low frequency trend in the data (does not change very fast/sporadically), whereas the additional modes capture higher frequency, lower magnitude variations in the data.
The reconstructed signal was then compared to the original signal using the following equation for the signal to noise ratio (SNR).
\[\text{SNR} = 10 \log_{10} \left( \frac{\sum_{i=1}^{N_f} f^2}{\sum_{i=1}^{N_f} (f - f_{\text{rec}})^2} \right)\]Note that this SNR metric penalizes any difference from the original signal. Thus, when the paper uses this SNR metric as the objective function when optimizing the VMD hyperparameters, the optimization will converge to the hyperparameters which result in a reconstructed signal that is most similar to the original, noisy signal, possibly capturing the noise in the reconstruction.
In the case of the paper, the true noiseless signal was unknown. However, for this study, the true signal was available. Thus, the following heatmaps of SNR vs. varying VMD hyperparameters were created.
Figure 4: Noisy Pressure SNR Heatmap
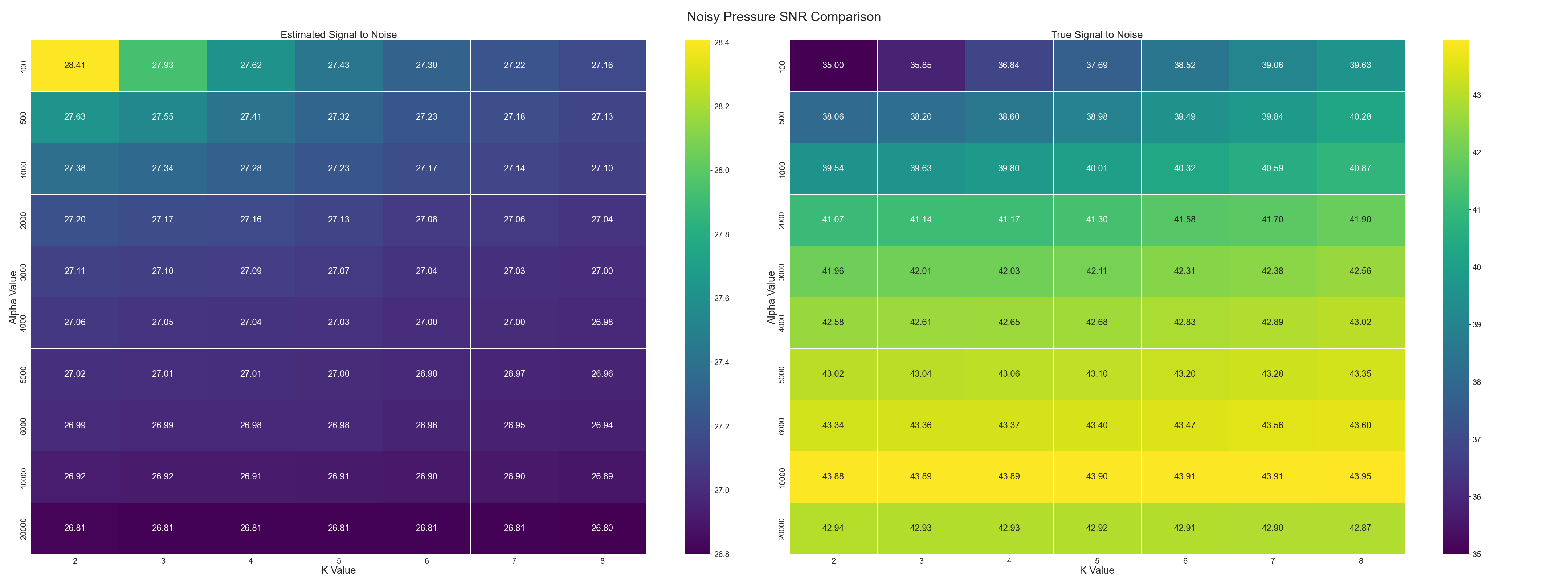
On the left, the reconstructed signal was compared to the original noisy signal (as performed in the paper), and on the right the reconstructed signal was compared to the original clean signal to see the true denoising potential of the methodology. As expected, the estimated SNR was maximized at a value of 28.41 with low α and k parameters, (100 and 2 respectively), which corresponds to limited change from the noisy signal. This is seen in the left side of Figure 4 where the yellow appears in the top left of the heatmap. The SNR of the reconstructed signal compared to the true noiseless signal is maximized at a value of 43.95 with α of 10,000 and k of 8. Thus, the methodology utilized in the paper is overly conservative in noise removal.
The following plot shows the comparison between the paper’s optimal reconstructed signal and the true optimal reconstructed signal.
Figure 5: Final Comparison Between Optimally Reconstructed Signals
In this figure it is clear to see that the reconstructed signal created with the paper’s methodology is less faithful to the original clean pressure signal, even though it has a higher estimated SNR. The true optimal signal is shown on the plot for comparison.
Conclusion
The exploration of variational mode decomposition (VMD) for denoising, inspired by the work of (Chen et al.), has revealed insights into the methodology’s strengths and limitations. The investigation focused on an artificial dataset with clean and noisy signals, utilizing VMD with varying hyperparameters α and k. The signal-to-noise ratio (SNR) was employed to assess denoising efficacy, distinguishing between estimated SNR (comparing the denoised signal to the noisy signal) and true SNR (comparing the denoised signal to the original clean signal).
The findings suggest that the paper’s denoising methodology, driven by the optimization of VMD hyperparameters using an SNR metric, tends to be overly conservative. The optimization process converges to hyperparameters that make minimal changes to the signal, resulting in a high estimated SNR but leaving room for a significant 25% improvement in true SNR.
VMD, in this context, essentially functions as a low-pass filter. While the methodology presented in the paper provides insights, alternative and simpler approaches such as a rolling average or a Butterworth filter may offer more practical solutions, being widely used and easier to interpret.
In conclusion, while VMD presents a viable denoising approach, careful consideration of hyperparameters is crucial. The study recommends reevaluating the optimization metric and exploring alternative methods that offer simplicity and widespread applicability.
Python Libraries
VMDpy
vmdpy is a library containing an implementation of VMD based off of the original paper by Dragomiretskiy & Zosso.
Numpy
Numpy is a powerhouse in scientific Python analysis, and needs no introduction.
Plotly
Plotly is a widely used plotting library which enables easy interactive plots which can be saved as interactive. They are the plots you’ll see embedded here.
Tqdm
Tqdm is just a progress bar library. I like to use it to let me know how long my scripts are taking.
Note: An environment.yml file is included in the GitHub repository to allow you to recreate a functional Anaconda environment.
References
The Steady State Detection Paper
This is the paper I was reading to learn about steady state detection where I found this method for first denoising the data.
The Original VMD Paper
This is the paper that originally proposed and explained VMD.